API¶
Classes¶
ESMPy uses a Field object to represent data variables
built on an underlying spatial discretization, which is represented by a
Grid, Mesh or
LocStream.
Regridding between Fields is accomplished with the
Regrid class. All of these classes are explained in
more detail in the sections provided by the links in the following table.
Class |
Description |
|---|---|
A manager class to initialize and finalize ESMF |
|
A class to represent a logically rectangular grid |
|
A class to represent an unstructured grid |
|
A class to represent observational data as a collection of disconnected points |
|
The regridding utility |
|
The from file regridding utility |
Named Constants¶
ESMPy follows the ESMF convention of using “named constants” to represent the available options for parameters that expect a variety of specific inputs. The following table lists the available named constants and provides links to pages that further explain the available values.
Named constants |
Description |
|---|---|
Specify the coordinate system of a |
|
Specify the format of a data file |
|
Specify a mask or area item on a |
|
Specify the type of line that connects two points on a sphere |
|
Specify how much logging should be done |
|
Specify the type of the |
|
Specify a nodal or elemental |
|
Specify the type of normalization to use for conservative regridding weights |
|
Specify the type of connection that appears at the poles of the |
|
Specify which type of artificial pole to construct on the source |
|
Specify various regions in the data layout of |
|
Specify which interpolation method to use regridding |
|
Specify the position for data in a |
|
Specify the type and kind of data |
|
Specify which action to take with respect to unmapped destination points |
Manager¶
The Manager is used by ESMPy to simplify a
number of low-level calls used by the underlying ESMF framework to allocate
resources, enable logging, and control garbage collection.
Resource Allocation¶
The ESMF Virtual Machine (VM) ESMF Virtual Machine (VM)
is created at the beginning of each ESMPy execution, and contains information
about the topology and characteristics of the underlying computer. The VM
allocates computational resources in the form of
Persistent Execution Threads, or PETs. These are equivalent to operating
system threads with a lifetime of at least that of the ESMPy execution. In the
simplest, and most common case, a PET is equivalent to an MPI process. The
number of PETs and the current PET can be queried from the
Manager:
mg = ESMF.Manager()
pet_count = mg.pet_count()
local_pet = mg.local_pet()
Logging¶
The Manager is also used to enable logging:
mg = ESMF.Manager(debug=True)
local_pet = mg.local_pet()
The output will be logged in files named PET<local_pet>.ESMF_LogFile.
Garbage Collection¶
The underlying ESMF framework needs to be initialized and finalized once and
only once per execution. This is handled internally by the
Manager and does not require any explicit
user intervention. However, the ESMF garbage collection feature is not triggered
until the finalization routine is invoked. So if memory deallocation of ESMPy
objects is required prior to the end of the program, the class level
destroy routines should be invoked:
mg = ESMF.Manager()
mg.destroy()
This is commonly required when reusing a Regrid object
to interpolate data between many Field pairs to
conserve memory to complete all interpolations in a single execution.
Spatial Discretization Objects¶
There are three different objects used for spatial coordinate representation:
Grid, Mesh, and LocStream. Grids are used to represent logically rectangular
grids, Meshes are used for unstructured collections of polygons, and
LocStreams are used for unstructured collections of individual points. These
objects are nearly identical counterparts to the objects of the same name in
ESMF, with some simplifications for ease of use in the Python environment.
Grid¶
The Grid is used to represent the geometry and discretization of logically
rectangular physical grids. The Grid can also hold information that can used in
calculations involving the Grid, like a mask or the cell areas. The ESMF reference
manual has an in-depth description of the
Grid class.
Staggering¶
Staggering is a finite difference technique in which the values of different physical quantities are placed at different locations within a grid cell.
The ESMF Grid class supports a variety of stagger locations, including cell
centers, corners, and edge centers. The default stagger location in ESMF is the
cell center, and cell counts in Grid are based on this assumption. Combinations
of the 2D ESMF stagger locations are sufficient to specify any of the Arakawa
staggers. ESMF also supports staggering in 3D and higher dimensions. There are
shortcuts for standard staggers, and interfaces through which users can create
custom staggers.
As a default the ESMF Grid class provides symmetric staggering, so that cell
centers are enclosed by cell perimeter (e.g. corner) stagger locations. This
means the coordinate arrays for stagger locations other than the center will
have an additional element of padding in order to enclose the cell center
locations. However, to achieve other types of staggering, the user may alter or
eliminate this padding by using the appropriate options when adding coordinates
to a Grid.
Grid staggers are indicated using
StaggerLoc.
grid = ESMF.Grid(np.array([3,4]), staggerloc=ESMF.StaggerLoc.CENTER)
Spherical Coordinates¶
In the case that the Grid is on a sphere (coord_sys = ESMF.api.constants.CoordSys.SPH_DEG or
ESMF.api.constants.CoordSys.SPH_RAD) then the coordinates given in the Grid are interpreted
as latitude and longitude values. The coordinates can either be in degrees or
radians as indicated by the coord_sys flag set during Grid creation. As is
true with many global models, this application currently assumes the latitude
and longitude refer to positions on a perfect sphere.
The Grid coordinate system is represented using
CoordSys.
grid = ESMF.Grid(np.array([3,4]), staggerloc=ESMF.StaggerLoc.CENTER,
coord_sys=ESMF.CoordSys.SPH_DEG)
Periodicity¶
A periodic connection can be specified when building Grids in spherical
coordinates. The num_peri_dims parameter indicates the total number of
periodic dimensions and periodic_dim is used to identify which dimensions
should be considered periodic. There must always be at least one non-periodic
dimension. For example, to create a global latitude-longitude Grid there would
be one periodic dimension, dimension 0 (longitude).
grid = ESMF.Grid(np.array([3,4]), staggerloc=ESMF.StaggerLoc.CENTER,
coord_sys=ESMF.CoordSys.SPH_DEG,
num_peri_dims=1, periodic_dim=0)
Pole Generation¶
The Grid can generate an artificial pole by using the pole_dim parameter. This
can be helpful for regridding operations to smooth out the interpolated values
in the polar region. For the example of creating a global latitude-longitude
Grid, the pole dimension would be 1 (latitude).
grid = ESMF.Grid(np.array([3,4]), staggerloc=ESMF.StaggerLoc.CENTER,
coord_sys=ESMF.CoordSys.SPH_DEG,
num_peri_dims=1, periodic_dim=0, pole_dim=1)
Masking¶
Masking is the process used to mark parts of a Grid to be ignored during an
operation. Marking Grid cells as masked can affect the Field values that are
represented by those cells. Masking is specified by assigning an integer value
to a Grid cell. This allows many different masks to be defined on the same Grid,
any combination of which may be also activated on the Field by specifying the
corresponding integer values. The activation of Field masks with respect to the
underlying Grid mask is handled by Regrid, and a more
general discussion of masking is covered in the masking
section.
In [1]: import numpy as np
...: import ESMF
...: grid = ESMF.Grid(np.array([3,4]), staggerloc=ESMF.StaggerLoc.CENTER,
...: coord_sys=ESMF.CoordSys.SPH_DEG,
...: num_peri_dims=1, periodic_dim=0, pole_dim=1)
...:
...: mask = grid.add_item(ESMF.GridItem.MASK, staggerloc=ESMF.StaggerLoc.CENTER)
...: mask
...:
Out[1]:
array([[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 1, 1, 1]], dtype=int32)
Cell Areas¶
Grid cell areas can be calculated by ESMPy. Space must first be allocated for
this calculation by adding an
AREA item to the Grid.
Then a Field must be created, and the
get_area() function called.
Grid cell areas may also be set to user-defined values
after the AREA item has
been allocated and retrieved using get_item().
In [1]: grid = ESMF.Grid(np.array([3,4]), staggerloc=[ESMF.StaggerLoc.CENTER, ESMF.StaggerLoc.CORNER],
...: coord_sys=ESMF.CoordSys.SPH_DEG,
...: num_peri_dims=1, periodic_dim=0, pole_dim=1)
...:
...:
...: gridLon = grid.get_coords(0)
...: gridLat = grid.get_coords(1)
...: gridLonCorner = grid.get_coords(0, staggerloc=ESMF.StaggerLoc.CORNER)
...: gridLatCorner = grid.get_coords(1, staggerloc=ESMF.StaggerLoc.CORNER)
...:
...: lon = np.linspace(-120,120,3)
...: lat = np.linspace(-67.5, 67.5,4)
...: lon_corner = np.arange(-180,180,120)
...: lat_corner = np.linspace(-90, 90, 5)
...:
...: lonm, latm = np.meshgrid(lon, lat, indexing='ij')
...: lonm_corner, latm_corner = np.meshgrid(lon_corner, lat_corner, indexing='ij')
...:
...: gridLon[:] = lonm
...: gridLat[:] = latm
...: gridLonCorner[:] = lonm_corner
...: gridLatCorner[:] = latm_corner
...:
...: field = ESMF.Field(grid)
...: field.get_area()
...: field.data
...:
Out[1]:
array([[ 0.32224085, 1.02707409, 1.02707409, 0.32224085],
[ 0.32224085, 1.02707409, 1.02707409, 0.32224085],
[ 0.32224085, 1.02707409, 1.02707409, 0.32224085]])
Mesh¶
A Mesh is an object for representing unstructured grids. The ESMF reference
manual has an in-depth description of the
Mesh class.
A Mesh is constructed of nodes and elements. A node, also known as a vertex
or corner, is a part of a Mesh which represents a single point. An element,
also known as a cell, is a part of a Mesh which represents a small
region of space. Elements are described in terms of a connected set of nodes
which represent locations along their boundaries.
Field data may be located on either the nodes or elements of a Mesh. Fields
created on a Mesh can also be used as either the source or destination or both
of a regridding operation.
The dimension of a Mesh in ESMF is specified with two parameters: the
parametric dimension and the spatial dimension.
The parametric dimension of a Mesh is the dimension of the topology of the Mesh.
This can be thought of as the dimension of the elements which make up the Mesh.
For example, a Mesh composed of triangles would have a parametric dimension of
2, and a Mesh composed of tetrahedra would have a parametric dimension of 3.
The spatial dimension of a Mesh is the dimension of the space in which the Mesh
is embedded. In other words, it is the number of coordinate dimensions needed to
describe the location of the nodes making up the Mesh.
For example, a Mesh constructed of squares on a plane would have a parametric
dimension of 2 and a spatial dimension of 2. If that same Mesh were used to
represent the 2D surface of a sphere, then the Mesh would still have a
parametric dimension of 2, but now its spatial dimension would be 3.
Only Meshes whose number of coordinate dimensions (spatial dimension) is 2 or 3
are supported. The dimension of the elements in a Mesh (parametric dimension) must
be less than or equal to the spatial dimension, but also must be either 2 or 3.
This means that a Mesh may be either 2D elements in 2D space, 3D elements in 3D
space, or a manifold constructed of 2D elements embedded in 3D space.
For a parametric dimension of 2, the native supported element types are
triangles and quadrilaterals. In addition to these, ESMF supports 2D polygons
with any number of sides. Internally these are represented as sets of triangles,
but to the user should behave like any other element. For a parametric dimension
of 3, the supported element types are tetrahedrons and hexahedrons. The Mesh
supports any combination of element types within a particular dimension, but
types from different dimensions may not be mixed. For example, a Mesh cannot be
constructed of both quadrilaterals and tetrahedra.
Mesh Creation¶
To create a Mesh we need to set some properties of the Mesh as a whole, some
properties of each node in the Mesh and then some properties of each element
which connects the nodes.
For the Mesh as a whole we set its parametric dimension and spatial dimension.
A Mesh's parametric dimension can be thought of as the dimension of the elements
which make up the Mesh. A Mesh's spatial dimension, on the other hand, is the
number of coordinate dimensions needed to describe the location of the nodes
making up the Mesh.
The structure of the per node and element information used to create a Mesh is
influenced by the Mesh distribution strategy. The Mesh class is distributed by
elements. This means that a node must be present on any PET that contains
an element associated with that node, but not on any other PET (a node
can’t be on a PET without an element “home”). Since a node may be used by
two or more elements located on different PETs, a node may be duplicated
on multiple PETs. When a node is duplicated in this manner, one and only
one of the PETs that contain the node must “own” the node. The user sets
this ownership when they define the nodes during Mesh
creation. When a Field is created on a
Mesh (i.e. on the Mesh nodes),
on each PET the Field is only
created on the nodes which are owned by that PET. This means that the size
of the Field memory on the PET can be smaller than the
number of nodes used to create the Mesh on that PET.
Three properties need to be defined for each Mesh node: the global id of the node
(node_ids), node coordinates (node_coords), and which PET owns the node
(node_owners). The node id is a unique (across all PETs) integer attached
to the particular node. It is used to indicate which nodes are the same when
connecting together pieces of the Mesh on different PETs. The node
coordinates indicate the location of a node in space and are used in the Regrid
functionality when interpolating. The node owner indicates which PET is in
charge of the node. This is used when creating a Field on the Mesh to indicate
which PET should contain a Field location for the data.
Three properties need to be defined for each Mesh element: the global id of the
element (element_ids), the topology type of the element (element_types), and
which nodes are connected together to form the element (element_conn). The
element id is a unique (across all PETs) integer attached to the
particular element. The element type describes the topology of the element
(e.g. a triangle vs. a quadrilateral). The range of choices for the topology of
the elements in a Mesh are restricted by the Mesh's parametric dimension (e.g. a
Mesh can’t contain a 2D element like a triangle, when its parametric dimension
is 3D), but it can contain any combination of elements appropriate to its
dimension. In particular, in 2D ESMF supports two native element types triangle
and quadrilateral, but also provides support for polygons with any number of
sides. These polygons are represented internally as sets of triangles, but to
the user should behave like other elements. To specify a polygon with more than
four sides, the element type should be set to the number of corners of the
polygon (e.g. element type=6 for a hexagon). The element connectivity indicates
which nodes are to be connected together to form the element. The number of
nodes connected together for each element is implied by the elements topology
type (element_types). It is IMPORTANT to note, that the entries in this list are
NOT the global ids of the nodes, but are indices into the PET local lists
of node info used in the Mesh creation. In other words, the element connectivity
isn’t specified in terms of the global list of nodes, but instead is specified
in terms of the locally described node info. One other important point about
connectivities is that the order of the nodes in the connectivity list of an
element is important. In general, when specifying an element with parametric
dimension 2, the nodes should be given in counterclockwise order around the
element.
The three step Mesh creation process starts with a call to the Mesh constructor.
It is then followed by the add_nodes() call to
specify nodes, and then the add_elements() call to
specify elements.
# 2.5 8 10 --------11
# / \ / |
# 2.1 7 9 12
# | | 5 /
# | 4 | /
# | | /
# 1.0 4 ------- 5 ------- 6
# | | \ 3 |
# | 1 | \ |
# | | 2 \ |
# -0.1 1 ------- 2 ------- 3
#
# -0.1 1.0 2.1 2.5
#
# Node Ids at corners
# Element Ids in centers
# Two parametric dimensions, and two spatial dimensions
mesh = ESMF.Mesh(parametric_dim=2, spatial_dim=2, coord_sys=coord_sys)
num_node = 12
num_elem = 5
nodeId = np.array([1,2,3,4,5,6,7,8,9,10,11,12])
nodeCoord = np.array([-0.1,-0.1, #node id 1
1.0,-0.1, #node id 2
2.1,-0.1, #node id 3
0.1, 1.0, #node id 4
1.0, 1.0, #node id 5
2.1, 1.0, #node id 6
0.1, 2.1, #node id 7
0.5, 2.5, #node id 8
1.0, 2.1, #node id 9
1.5, 2.5, #node id 10
2.5, 2.5, #node id 11
2.5, 2.1]) #node id 12
nodeOwner = np.zeros(num_node)
elemId = np.array([1,2,3,4,5])
elemType=np.array([ESMF.MeshElemType.QUAD,
ESMF.MeshElemType.TRI,
ESMF.MeshElemType.TRI, 5, 6])
elemConn=np.array([0,1,4,3, # elem id 1
1,2,4, # elem id 2
2,5,4, # elem id 3
3,4,8,7,6, # elem id 4
4,5,11,10,9,8]) # elem id 5
mesh.add_nodes(num_node,nodeId,nodeCoord,nodeOwner)
mesh.add_elements(num_elem,elemId,elemType,elemConn)
Masking¶
There are two types of masking available in Mesh: node masking and element
masking. These both work in a similar manner, but vary slightly in the details
of setting the mask information during Mesh creation.
For node masking, the mask information is set using the node_mask parameter.
When a Regrid object is created the mask values arguments src_mask_values and
dst_mask_values can then be used to indicate which particular values set in
the node_mask array indicate that the node should be masked. For example, if
dst_mask_values has been set to 1, then any node in the destination Mesh whose
corresponding node_mask value is 1 will be masked out (a node with any other
value than 1 will not be masked).
For element masking, the mask information is set using the element_mask
parameter when adding elements to the Mesh. In a similar manner to node masking,
the mask values parameters to Regrid, src_mask_values and dst_mask_values
can then be used to indicate which particular values set in the element_mask
array indicate that the element should be masked. For example, if
dst_mask_values has been set to 1, then any element in the destination Mesh
whose corresponding element_mask value is 1 will be masked out (an element
with any other value than 1 will not be masked).
Areas¶
Mesh cell areas can be specified using the element_areas parameter to
add_elements().
If cell areas are not specified by the user they can be calculated by ESMPy
using get_area().
LocStream¶
A LocStream can be used to represent the locations of a set of
data points. For example, in the data assimilation world, LocStreams can be used
to represent a set of observations. The values of the data points are stored
within a Field created using the LocStream. The ESMF reference
manual has an in-depth description of the
LocStream class.
The locations are generally described using Cartesian (x, y, z), or
(lat, lon, radius) coordinates. The coordinates are stored using constructs
called keys. A key is essentially a list of point descriptors, one for each data
point. They may hold other information besides the coordinates - a mask, for
example. They may also hold a second set of coordinates. Keys are referenced by
name. Each key must contain the same number of elements as there are data points
in the LocStream. While there is no assumption in the ordering of the points,
the order chosen must be maintained in each of the keys.
A LocStream can be very large. Data assimilation systems might use LocStreams
with up to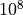 
observations, so efficiency is critical. LocStreams can be
created from file.
A LocStream is similar to a Mesh in that both are collections of irregularly
positioned points. However, the two structures differ because a Mesh also has
connectivity: each data point represents either a center or corner of a cell.
There is no requirement that the points in a LocStream have connectivity, in
fact there is no requirement that any two points have any particular spatial
relationship at all.
locstream = ESMF.LocStream(16, coord_sys=coord_sys)
deg_rad = pi
if coord_sys == ESMF.CoordSys.SPH_DEG:
deg_rad = 180
locstream["ESMF:Lon"] = [0.0, 0.5*deg_rad, 1.5*deg_rad, 2*deg_rad, 0.0, 0.5*deg_rad, 1.5*deg_rad, 2*deg_rad, 0.0, 0.5*deg_rad, 1.5*deg_rad, 2*deg_rad, 0.0, 0.5*deg_rad, 1.5*deg_rad, 2*deg_rad]
locstream["ESMF:Lat"] = [deg_rad/-2.0, deg_rad/-2.0, deg_rad/-2.0, deg_rad/-2.0, -0.25*deg_rad, -0.25*deg_rad, -0.25*deg_rad, -0.25*deg_rad, 0.25*deg_rad, 0.25*deg_rad, 0.25*deg_rad, 0.25*deg_rad, deg_rad/2.0, deg_rad/2.0, deg_rad/2.0, deg_rad/2.0]
if domask:
locstream["ESMF:Mask"] = np.array([1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], dtype=np.int32)
Create a Grid or Mesh from File¶
File Formats¶
ESMPy can create Grid or Mesh objects from NetCDF files in a variety
of formats. A Mesh can be created from files in SCRIP, ESMFMESH, and UGRID
formats. Grid files can be in SCRIP and GRIDSPEC format.
SCRIP¶
This file format is used by the SCRIP [1], package, grid files that
work with that package should also work here. SCRIP format files are
capable of storing either 2D logically rectangular grids or 2D
unstructured grids. More information can be found in the ESMF reference
manual section on the SCRIP Grid File Format.
ESMFMESH¶
ESMF has a custom unstructured grid file format for describing Meshes.
This format is more compatible than the SCRIP format with the methods
used to create a Mesh object, so less conversion needs to be done to
create a Mesh. The ESMFMESH format is thus more efficient than SCRIP when
used with ESMPy. More information can be found in the ESMF reference
manual section on the ESMF Unstructured Grid File Format.
GRIDSPEC¶
GRIDSPEC is an extension to the Climate and Forecast (CF) metadata
conventions for the representation of gridded data for Earth System
Models. ESMPy supports NetCDF files that follow the CF GRIDSPEC
convention to support logically rectangular lat/lon grids. More
information can be found in the ESMF reference manual section on the
CF Convention GRIDSPEC File Format.
UGRID¶
UGRID is an extension to the CF metadata
conventions for the unstructured grid data model. ESMPy support
NetCDF files that follow the CF UGRID convention for unstructured grids.
More information can be found in the ESMF reference manual section on
the CF Convention UGRID File Format.
Meshes from File¶
When creating a Mesh from a SCRIP format file, there are a number of
options to control the output Mesh. The data is located at the center
of the grid cell in a SCRIP grid. Therefore, when the Mesh will be
part of a conservative regridding operation, the convert_to_dual
flag must be set to True to properly generate coordinates at the the
cell corners.
A Mesh may also be created with boolean flags to specify whether or not to
add an area property to the Mesh add_user_area, or to add a mask
add_mask held by the NetCDF variable indicated in the optional argument,
varname. These argument are only valid for UGRID formatted files.
The mask generated for a Mesh created from file will
have 0 for the masked values and 1 for the unmasked values.
Grids from File¶
A number of optional boolean arguments are also supported to create a
structured Grid from a file. These include is_sphere to indicate whether
the grid is spherical or regional, add_corner_stagger to add the corner
stagger information to the Grid for conservative regridding, and
add_user_area to specify whether to read in the cell area from the
NetCDF file or to calculate them.
For GRIDSPEC formated files
there is the add_mask optional argument
to add a mask held by the NetCDF variable indicated in optional
argument, varname, and the coord_names argument to specify the longitude
and latitude variable names in a GRIDSPEC file containing multiple sets of
coordinates.
For SCRIP formated files the integer array grid_imask is used to mask out grid cells which should not participate in the regridding.
The mask generated for a Grid created from
file (any format) will have 0 for the masked values and 1 for the unmasked values.
Regridding¶
The following table describe the regridding methods and options that are available in ESMPy, the flag that is required to use it, a short description, and an ESMF documentation reference.
Class |
Description |
Link |
|---|---|---|
Linear regridding in two dimensions |
||
Higher-order least squares method |
||
Nearest source point used for each destination |
||
Nearest destination point used for each source |
||
First-order conservative |
||
Second-order conservative |
||
See conservative options above. |
Conservation equations |
|
Normalization options for integral conservation |
||
Line types for spherical and Cartesian space |
||
Unmapped destination point handling options |
||
Spherical grids and pole handling |
Masking¶
Masking is the process whereby parts of a Grid, Mesh or LocStream can be marked to be ignored
during an operation, such as when they are used in regridding. Masking can be used on a Field
created from a regridding source to indicate that certain portions should not be used to generate
regridded data. This is useful, for example, if a portion of the source contains unusable values.
Masking can also be used on a Field created from a regridding destination to indicate that a certain
portion should not receive regridded data. This is useful, for example, when part of the destination
isn’t being used (e.g. the land portion of an ocean grid).
The user may mask out points in the source Field or destination Field or both. To do masking the user
sets mask information in the Grid, Mesh, or LocStream upon
which the Fields passed into the Regrid call are built. The src_mask_values and
dst_mask_values arguments to that call can then be used to specify which values in that mask information
indicate that a location should be masked out. For example, if dst_mask_values is set to [1,2], then any
location that has a value of 1 or 2 in the mask information of the Grid, Mesh or LocStream upon which
the destination Field is built will be masked out.
Masking behavior differs slightly between regridding methods. For non-conservative regridding methods
(e.g. bilinear or high-order patch), masking is done on points. For these methods, masking a destination
point means that the point will not participate in regridding. For these
methods, masking a source point means that the entire source cell using that point is masked out.
In other words, if any corner point making up a source cell is masked then the cell is masked.
For conservative regridding methods masking is done on cells.
Masking a destination cell means that the cell won’t participate in regridding.
Similarly, masking a source cell means that the cell won’t participate in regridding.
For any type of interpolation method (conservative or non-conservative)
the masking is set on the location upon which the
Fields passed into the regridding call are built.
For example, if Fields built on
StaggerLoc.CENTER are passed into
Regrid
then the masking should also be set on StaggerLoc.CENTER.
The mask generated for a Grid,
Mesh or LocStream created
from file will have 0 for the masked values and 1 for the unmasked values.
Numpy Slicing and Indexing¶
Numpy arrays are used to represent Grid, Mesh and LocStream coordinates and Field data,
among other things. Standard numpy conventions for array indexing
and slicing can be expected. There are some exceptions when it comes to fancy
indexing, index arrays, and multi-dimensional slicing. Significant effort has
been put into raising exceptions where inappropriate indexing or slicing
operations are attempted.
It is very important to remember that all indexing
and slicing operations apply ONLY to the ESMPy level objects, and these operations
do not propagate down to the lower-level Fortran- and C-based representations
of the ESMF objects. One example of where this could come up is when passing
a Field slice into regridding. The entire original Field will still be run
through the ESMF regridding engine, and only the appropriate portion of
the Field slice will be updated with the regridded values.
Dimension Ordering¶
Warning
The underlying ESMF library is built with a mix of Fortran and C/C++ and follows Fortran conventions with respect to array indexing and dimension ordering. Some effort has been made to make ESMPy feel more natural to the Python user where possible. This means that ESMPy uses 0-based indexing, which is translated to the 1-based indexing used by the ESMPy backend. However, the dimension ordering still follows Fortran conventions. Namely, longitude comes before latitude, which also comes before temporal dimensions when in use.
In [1]: import numpy as np
...: import ESMF
...:
...: grid = ESMF.Grid(np.array([3,4]), staggerloc=ESMF.StaggerLoc.CENTER)
...:
...: gridLon = grid.get_coords(0)
...: gridLat = grid.get_coords(1)
...:
...: lon = np.linspace(-120,120,3)
...: lat = np.linspace(-67.5, 67.5,4)
...:
...: lonm, latm = np.meshgrid(lon, lat, indexing='ij')
...:
...: gridLon[:] = lonm
...: gridLat[:] = latm
...:
In [2]: grid.coords[ESMF.StaggerLoc.CENTER][0].shape
Out[2]: (3, 4)
In [3]: lon.shape
Out[3]: (3,)
In [4]: lat.shape
Out[4]: (4,)
In [5]: grid.coords[ESMF.StaggerLoc.CENTER][0]
Out[5]:
array([[-120., -120., -120., -120.],
[ 0., 0., 0., 0.],
[ 120., 120., 120., 120.]])
In [6]: grid.coords[ESMF.StaggerLoc.CENTER][1]
Out[6]:
array([[-67.5, -22.5, 22.5, 67.5],
[-67.5, -22.5, 22.5, 67.5],
[-67.5, -22.5, 22.5, 67.5]])
In [7]: field = ESMF.Field(grid, ndbounds=[10]) # create a Field with a time dimension
In [8]: field.data.shape
Out[8]: (3, 4, 10)
Parallel Execution¶
ESMPy is a thin wrapper on top of ESMF, which was designed for high performance and scalable computing. The ESMF virtual machine is used to manage the available resources of the execution environment in a layer that is transparent to the ESMPy user. This allows the full power of the high performance computing environment to be utilized by the ESMPy user with little use of specialized parallel programming techniques.
ESMPy objects will be distributed across the available computing resources with
no additional parameters required. The Grid, Mesh, LocStream, and Field classes
will all be transparently “parallelized” with no need for user calls to a
message passing interface. Likewise, the Regrid class will compute and apply
the interpolation weights using all available computing resources with no need
for user intervention.
However, it is useful to remember that resulting Field values will only be
accessible on certain PETs. The mpi4py package may be necessary for post
processing tasks that require access to global Field values.
mpirun vs. MPI.Spawn¶
There are a few different options for using ESMPy in a parallel environment. Using mpirun to specify the desired number of computing cores is probably the easiest way to start a parallel ESMPy job. Another option is to call the MPI.Spawn() function from the mpi4py Python package from within a serial Python script or interpreter. It has been observed that MPI.Spawn() may not work properly when mpi4py is built with an underlying mpich library, openmpi has seen better success. A third option is to call mpirun using a system call from within a serial Python script or interpreter, however this method is not highly recommended.
The following two examples demonstrate how to execute an ESMPy script in parallel. Any of the scripts found in the examples directory of the ESMPy source code can be run in parallel using mpirun as well as in serial mode.
mpirun¶
mpirun -n 4 python hello_world.py
MPI.Spawn¶
import sys
from mpi4py import MPI
# Parent
if len(sys.argv) == 1:
# Spawn workers
comm = MPI.COMM_WORLD.Spawn(
sys.executable,
args=[sys.argv[0], 'worker'],
maxprocs=4)
# Shutdown
comm.Disconnect()
# Worker
elif sys.argv[1] == 'worker':
# Connect to parent
try:
comm = MPI.Comm.Get_parent()
rank = comm.Get_rank()
except:
raise ValueError('Could not connect to parent - ' + usage)
# worker code goes here, regridding etc..
print "Hello World from PET #"+str(rank)
# Shutdown
comm.Disconnect()
# Catch
else:
raise ValueError('Program should be started without arguments')
A more detailed example of using MPI.Spawn() can be found in the Tutorials section of the documentation.